Denksportaufgaben

Pumpen und Wasserbecken	[Lösung]

Drei Pumpen A, B und C arbeiten mit unterschiedlicher Leistung. Zum Füllen des Beckens benötigen sie zusammen eine Stunde. Eines Morgens werden sie um 8.00 Uhr in Betrieb gesetzt, um 8.30 Uhr wird Pumpe A abgeschaltet. Die Pumpen B und C benötigen noch bis 9.20 Uhr, um das Becken vollständig zu füllen. Am nächsten Tag soll das Becken allein durch A gefüllt werden.

Wie lange dauert dies?

La Pyramide Mystérieuse	[Lösung]

     

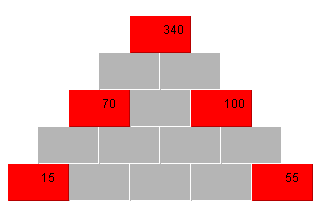
Der Wert eines Steines errechnet sich immer aus der Summe der beiden darunter liegenden Steine.

Wie lauten die fehlenden Werte? (Dieses Rätsel ist aus einer französischen Boulevard-Zeitung)

Wer sagt die Wahrheit?	[Lösung]

Paul sagt: "Max lügt."
Max sagt: "Otto lügt."
Otto sagt: "Max und Paul lügen."

Wer lügt hier wirklich und wer sagt die Wahrheit?

1. Paul und Otto lügen, Max sagt die Wahrheit
2. Paul lügt, Otto und Max sagen die Wahrheit
3. Max lügt, Paul und Otto sagen die Wahrheit
4. Max und Otto lügen, Paul sagt die Wahrheit

Komplizierte Familienverhältnisse	[Lösung]

Am Mittagstisch sitzen ein Großvater, eine Großmutter, zwei Väter, zwei Mütter, vier Kinder, drei Enkel, ein Bruder, zwei Schwestern, zwei Söhne, zwei Töchter, ein Schwiegervater, eine Schwiegermutter und eine Schwiegertochter.

Wie viele Teller werden mindestens benötigt?

Programmiersprache BLOED	[Lösung]

In der Programmiersprache BLOED hat man nur die folgenden sechs Befehle zur Verfügung:

READ(x)	Liest eine reelle Variable x ein.
WRITE(x)	Schreibt den Wert der Variablen x auf den Bildschirm.
z = PLUS(x,y)	Weist der Variable z die Summe aus x und y zu.
z = MINUS(x,y)	Weist der Variable z die Differenz aus x und y zu.
z = DIVIDE(x,i)	Weist z den Quotienten aus x und i zu.
z = CUBE(x)	Weist z den Wert x * x * x zu.

Erstellen Sie mit der Programmiersprache BLOED ein Programm, das zu Beginn drei Variablen a,b und c einliest und am Ende den Wert des Produktes a * b * c ausgibt!

Zahlenfolge I	[Lösung]

Ergänzen Sie folgende Zahlenfolge, die in der Zeitschrift "Spiegel" in der Ausgabe Nr. 38/1997 erschienen ist, um ein weiteres Element:

1, 2, 5, 8, 15, 28, 51, 94, ...

Zahlenfolge II	[Lösung]

1, 3, 6, 11, 18, 29, 42, 59, 78, ...

Fahren Sie fort!

Zahlenfolge III	[Lösung]

1, 2, 4, 8, 16, 23, 28, 38, 49, ...

Fahren Sie fort!

Rechnung aufstellen	[Lösung]

Gegeben sind die Ziffern 1,5,6 und 7 und beliebig viele (, ), +, -, *, / (Rechenzeichen und Klammern)

Stellen Sie damit eine Rechnung auf, deren Ergebnis 21 ergibt! Jede Ziffer darf nur einmal verwendet werden.

Eine interessante Telefonnummer	[Lösung]

Zwei alte Schulkameraden treffen sich nach langen Jahren zufällig beim Einkaufen mit ihren Frauen. Da sie sich mehr zu erzählen haben, als in der kurzen Zeit möglich ist tauschen Sie die Telefonnummern aus. Als Sepp die Nummer von Hans sieht, meint er, dass er sich die Nummer schwer merken könne, weil sie so langweilig sei. Daraufhin erwiedert Hans (er ist Mathe-Lehrer): "Es gibt keine langweiligen Zahlen! Meine Telefonnummer ist wie Du siehst sechsstellig. Wenn Du die letzte Ziffer wegnimmst und vor die restlichen 5 Ziffern stellst, so ist die neue Nummer exakt 5 Mal so groß wie meine Telefonnummer!"

Wie lautet nun die Telefonnummer von Hans?

Die Kunst des Teilens	[Lösung]

***	*	***	: ** = **8**
***
	*	*
	*	*
		***
		***

Dies stellt eine Divisionsaufgabe dar, wobei ein Sternchen für jeweils eine Ziffer steht.

Wie lautet der Dividend der Aufgabe?

Die zwei Türen	[Lösung]

Ein sadistischer Tyrann hat einen Denker ins Gefängnis gesperrt. Die Zelle des Denkers hat zwei Türen. Eine führt in die Freiheit, die andere in den Tod. Vor jeder der beiden Türen steht ein Wächter. Einer der beiden sagt immer nur die Wahrheit, der andere immer nur die Unwahrheit. Wer welcher ist, weiß der Denker nicht. Aber er darf nur einem der Wächter eine einzige Frage stellen, um sich zu befreien. Schon Minuten später spaziert er fröhlich und frei über den Marktplatz.

Welche Frage hat der Denker gestellt?

Drei Häftlinge	[Lösung]

In einem Gefängnis saßen drei Häftlinge. Der Erste hatte zwei Augen, der Zweite nur noch Eines, der Dritte war ganz blind. Der Gefängnisdirektor kündigte den Dreien an, dass er von einer Sammlung von drei weißen und zwei blauen Hüten drei Hüte auswählen werde, um sie den Häftlingen aufzusetzen. Sie wurden dabei aber gehindert, die Farbe des Hutes zu sehen, der ihnen selbst aufgesetzt wurde. Dann wurden die Häftlinge zusammengebracht und der Gefängnisdirektor versprach dem normal Sehenden die Freiheit, wenn er die Farbe seines eigenen Hutes angeben könne. Der Häftling gestand ein, dass er dies nicht könne. Nun kam der Einäugige an die Reihe. Auch er musste dasselbe eingestehen. Der Direktor gab sich nicht damit ab, den Blinden zu fragen, aber als dieser ihn anflehte, willigte er ein, die gleichen Bedingungen auch für ihn gelten zu lassen. Der Blinde grinste breit und sprach:

"Was ich von meinen Freunden weiß, das lässt mich sehen ganz genau auch ohne Augen: mein Hut ist ..."

Ergänzen Sie den Spruch und begründen Sie Ihre Antwort!

Herr Summe und Herr Produkt	[Lösung]

Eine wirklich interessante Aufgabe aus dem "Selbsttest zur Prüfung der Eignung zum Studium der Informatik" der TU München:

Zu finden sind zwei natürliche ganze Zahlen, die beide zwischen 1 und 100 liegen. Eine Person, im folgenden "Herr Produkt" genannt, kennt das Produkt der beiden Zahlen, eine andere Person, im folgenden "Herr Summe" genannt, kennt ihre Summe. Zwischen den beiden Personen entwickelt sich der folgende Dialog:

Herr Produkt: "Ich kenne die beiden Zahlen nicht."
Herr Summe: "Ich kenne die beiden Zahlen auch nicht, ich wusste aber, daß Sie sie nicht kennen."
Herr Produkt: "Dann kenne ich die beiden Zahlen jetzt."
Herr Summe: "Dann kenne ich die beiden Zahlen jetzt auch."

Welches sind die beiden Zahlen?

Einsteins Rätsel	[Lösung]

Einstein verfasste dieses Rätsel im letzten Jahrhundert. Er behauptete 98% der Weltbevölkerung seien nicht in der Lage es zu lösen. Gehören Sie zu den 2% der intelligentesten Personen auf der Welt? Es gibt keinen Trick bei diesem Rätsel, nur pure Logik. Viel Spaß beim Ausprobieren...

Ausgangssituation:

1.	Es gibt fünf Häuser mit je einer anderen Farbe.
2.	In jedem Haus wohnt eine Person einer anderen Nationalität.
3.	Jeder Hausbewohner bevorzugt ein bestimmtes Getränk, raucht eine bestimmte Zigarettenmarke und hält ein bestimmtes Haustier.
4.	KEINE der fünf Personen trinkt das gleiche Getränk, raucht die gleichen Zigaretten oder hält das gleiche Tier wie einer seiner Nachbarn.

Ihre Hinweise:

1.	Der Brite lebt im roten Haus.
2.	Der Schwede hält einen Hund.
3.	Der Däne trinkt gerne Tee.
4.	Das grüne Haus steht links vom weißen Haus.
5.	Der Besitzer des grünen Hauses trinkt Kaffee.
6.	Die Person, die Pall Mall raucht, hält einen Vogel.
7.	Der Mann, der im mittleren Haus wohnt, trinkt Milch.
8.	Der Norwege wohnt im ersten Haus.
9.	Der Marlboro-Raucher wohnt neben dem, der eine Katze hält.
10.	Der Besitzer des gelben Hauses raucht Dunhill.
11.	Der Mann, der ein Pferd hält, wohnt neben dem, der Dunhill raucht.
12.	Der Winfield-Raucher trinkt gerne Bier.
13.	Der Norweger wohnt neben dem blauen Haus.
14.	Der Deutsche raucht Rothmanns.
15.	Der Marlboro-Raucher hat einen Nachbarn, der Wasser trinkt.

Fragestellung: Wem gehört der Fisch?

Lösungshinweis:
Die Zeitschrift P.M. Magazin beinhaltet in jeder Ausgabe einen "Logiktrainer". Dies ist jedesmal eine Aufgabe vom selben Typ wie Einsteins Rätsel. Im Heft werden auch Hinweise für die Lösung eines solchen Aufgabentyps gegeben.